Description
Design And Analysis Of An OFDM-Based Orthogonal Chaotic Vector Shift Keying Communication System
ABSTRACT
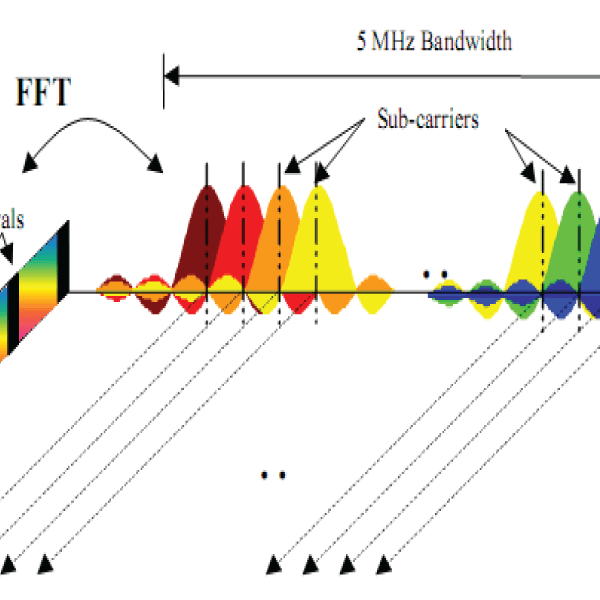
We propose a new non-coherent multicarrier spread-spectrum system that combines orthogonal chaotic vector shift keying (OCVSK) and orthogonal frequency division multiplexing (OFDM). The system enhances OCVSK by sending multiple groups of information sequences with the same orthogonal chaotic vector reference sequences over the selected subcarriers. Does each group carry? information bits and is separated from other groups by orthogonal chaotic reference signals. We derive the information rate enhancement (IRE) and the energy saving enhancement (ESE) factors as well as the bit error rate (BER) theory of OFDM-OCVSK under additive white Gaussian noise (AWGN) and multipath Rayleigh fading channels and compare the results with conventional OCVSK systems. Design And Analysis Of An OFDM-Based Orthogonal Chaotic Vector Shift Keying Communication System Design And Analysis Of An OFDM-Based Orthogonal Chaotic Vector Shift Keying Communication System Design And Analysis Of An OFDM-Based Orthogonal Chaotic Vector Shift Keying Communication System
Design And Analysis Of An OFDM-Based Orthogonal Chaotic Vector Shift Keying Communication System
INTRODUCTION
Over the past decade, chaos-based wireless digital communication systems have attracted increasing research interest. The sensitivity of chaotic signals to initial conditions allows infinite numbers of independent signals to be generated easily at low cost, with high security and a good degree of randomness. Furthermore, chaotic systems have large bandwidth, low power spectral density, and immunity against multipath fading channels and jamming coupled with a low probability of interception. One of the most popular non-coherent chaos modulation techniques for communication systems is differential chaos shift keying. Unlike coherent chaos shift keying (CSK), DCSK is able to detect the transmitted bits without requiring any synchronization or channel state information (CSI) on the receiver side.
In order to use chaotic processes, it is necessary to understand the nature of these systems, at a basic level, to utilize them successfully for communications schemes. Section (2.2) introduces some basic ideas and necessary properties of chaotic systems and briefly describes their underlying properties. Design And Analysis Of An OFDM-Based Orthogonal Chaotic Vector Shift Keying Communication System
Design And Analysis Of An OFDM-Based Orthogonal Chaotic Vector Shift Keying Communication System
EXISTING SYSTEM
- The Symmetric Chaos Shift Keying (SCSK): The principal disadvantage of this approach, and the derivation of its name, is the requirement that the chaotic process is an even or symmetric function in a single or some combination of states. This requirement comes from the need for the receiver to be able to synchronize with the received signal, regardless of the sign of the bit code.
- Correlation Delay Shift Keying (CDSK): The disadvantage of this approach is that the noise rejection is not as good as DCSK.
- Differential Chaos Shift Keying (DCSK): This approach has good noise rejection but is flawed by a need for the receiver to be in phase with the transmitter. Design And Analysis Of An OFDM-Based Orthogonal Chaotic Vector Shift Keying Communication System
Design And Analysis Of An OFDM-Based Orthogonal Chaotic Vector Shift Keying Communication System
PROPOSED SYSTEM
- We propose a new non-coherent multicarrier spread-spectrum system that combines orthogonal chaotic vector shift keying (OCVSK) and orthogonal frequency division multiplexing (OFDM). Does the system enhance OCVSK by sending multiple groups of information sequences with the same orthogonal chaotic vector reference sequences over the selected subcarriers.?
ADVANTAGES
- The PAPR performance of the proposed GFDM-CCSK waveform is obviously improved compared with traditional OFDM and GFDM.
- Meanwhile, the multi-code GFDMCCSK can effectively increase the access success ratio and reduce the average delay of the system.
Design And Analysis Of An OFDM-Based Orthogonal Chaotic Vector Shift Keying Communication System
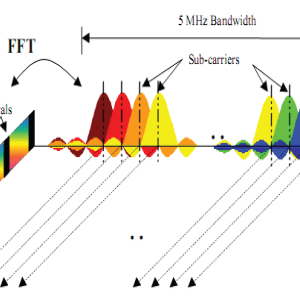
BLOCK DIAGRAM EXPLANATION
Consider the n? m signal matrix X produced by taking nm samples of the chaotic process. Where each set of n samples has the mean value removed thus leaving each vector of the matrix X as samples of a zero mean process. Now an orthonormal matrix U is generated from it using the Gram-Schmidt process The matrix U is multiplied by a diagonal power balancing matrix P to produce a matrix Q before being streamed. Streaming is transmitting each element of each column of the Q matrix in turning over the communication channel. And finally, the Bit Error Rate (BER), probability problem and the problems of signal characterization; and the signal-to-noise ratio effects on the BER, are derived in a new and novel way for each of the encoding schemes
Design And Analysis Of An OFDM-Based Orthogonal Chaotic Vector Shift Keying Communication System
SOFTWARE REQUIRED
MATLAB 2018 and above
REFERENCE
[1] G. Kaddoum, Wireless chaos-based communication systems: a comprehensive survey,? IEEE Access, vol. 4, pp. 2621?2648, 2016.
[2] Y. Xia, C. K. Tse, and F. C. M. Lau, Performance of differential chaos shift-keying digital communication systems over a multipath fading channel with delay spread,? IEEE Trans. Circuits Syst. II, vol. 51, no. 12, pp. 680?684, 2004.
[3] J. Yu and Y.-D. Yao, the Detection performance of chaotic spreading LPI waveforms,? IEEE Trans. Wireless Commun., vol. 4, no. 2, pp. 390?396, 2005.
[4] M. Z. Hasan, I. Idris, A. F. M. N. Uddin, and M. Shahjahan, ?Performance analysis of a coherent chaos-shift keying technique,? in Proc. 15th Int. Conf. Comput. Inf. Technol. (ICCIT), pp. 249?254, 2012.
[5] G. Kolumban, B. Vizv?ari, W. Schwarz, and A. Abel, ?Differential chaos shift keying: A robust coding for chaos communication,? in Proc. NDES96, pp. 87?92, 1996.
[6] Z. Zhou, T. Zhou, and J. Wang,? Exact BER analysis of differential chaos shift keying communication system in fading channels,? in Proc. 4th Int. Conf. Wireless Commun., Netw. Mobile Comput., pp. 1 4, 2008.
[7] T. J. Wren and T. C. Yang, ?Orthogonal chaotic vector shift keying in digital communications,? in IET Communications, vol. 4, no. 6, pp. 739-753, April 16 2010.
[8] G. Kolumban, M. P. Kennedy, G. Kis, and Z. Jako, ?FDISK: a novel method for chaotic communications,? in Proc. IEEE Int. Symp. Circuits Syst., ISCAS, vol. 4, pp. 477?480 vol. 4, 1998.
[9] M. P. Kennedy, G. Kolumban, G. Kis, and Z. Jako, ?Performance evaluation of FM-DCSK modulation in multipath environments,? IEEE Trans. Circuits Syst. I, vol. 47, no. 12, pp. 1702? 1711, 2000.
[10] Z. Galias and G. M. Maggio, ?Quadrature chaos-shift keying: theory and performance analysis,? IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, vol. 48, no. 12, pp. 1510? 1519, December 2001.
[12] Hua Yang and Guo-Ping Jiang, ?High-efficiency differential-chaos-shift-keying scheme for chaos-based noncoherent communication,? IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 59, no. 5, pp. 312? 316, April 2012.
[13] Hua Yang and Guo-Ping Jiang, ” Reference-modulated DCSK: a novel chaotic communication scheme,” IEEE Transactions on Circuits and Systems II: Express Briefs vol. 60, no. 4, pp. 232 ? 236, 2013.




































































































































































































































































































































































































































































































































































































































































































































































































































































































Customer Reviews
There are no reviews yet.